Fortune and misfortune
Press the button below to translate. Please, note that automatic translation is far to be perfect.

Quante volte vi sarà capitato di dire «Ma che sfortuna!» oppure «Guarda che fortuna, quello lì!». Per molti la fortuna e la sfortuna non esistono, sono solo interpretazioni soggettive di qualcosa che può essere perfettamente spiegato con la statistica; per altri, invece, è una realtà inconfutabile i cui segreti sono oggetto di studio di discipline esoteriche o misteriche come la chiromanzia o l’astrologia. Per i più è solo un modo di dire, anche se poi tutti noi ogni tanto siamo portati ad essere un po’ scaramantici, anche se alcuni non lo ammetteranno mai.
Ma allora, esistono o no la fortuna e la sfortuna?
Se vogliamo vedere la cosa da un punto di vista antropologico, la risposta non può che essere SÌ, dato che i concetti di fortuna e sfortuna sono ben definiti nella società umana, tanto che se ne può dare una definizione operativa, ovvero tale da poter usata da un punto di vista scientifico. Almeno è quello che ho intenzione di fare con questo articolo, ovvero definire in modo chiaro il significato di questi due termini così da poterli usare nell’ambito di un’eventuale studio di come l’essere umano si confronta con ciò che avviene attorno a lui.
Ovviamente, come tutte le definizioni, anche queste sono delle semplici convenzioni. Si possono accettare o meno, ovvero riconoscere che coprano più o meno in modo esaustivo tutta la casistica di situazioni nelle quali siamo portati ad utilizzarle ma, una volta accettate, quello che importa è che poi si rimanga coerenti ad esse.
Le due definizioni sono praticamente identiche, salvo per un termine, per cui analizziamo prima quella relativa alla sfortuna.
Dicasi sfortuna il verificarsi di uno o più eventi inconsueti o poco frequenti, le cui conseguenze abbiano un effetto negativo su uno o più individui.
Analizziamola in dettaglio.
Tanto per cominciare la sfortuna è sempre legata al verificarsi di qualcosa: non è cioè la conseguenza di un’azione diretta e facilmente attribuibile a un individuo, quanto piuttosto un evento le cui cause non sono riconducibili in modo chiaro a una volontà umana. Ad esempio, se prendo un sasso e lo tiro volutamente addosso a qualcuno prendendolo in pieno, difficilmente qualcuno parlerà di sfortuna, ma se lo stesso pezzo di pietra dovesse cadere da una parete rocciosa e colpisse in testa un ignaro passante, allora sarebbero in molti ad attribuire l’evento alla mala sorte.
Secondo, l’evento in questione deve avere una probabilità piuttosto bassa di verificarsi. Il soldato che viene mandato all’assalto delle mura del castello sotto il tiro continuo degli arcieri avversari ed è colpito in pieno da una freccia, non viene certo considerato un uomo sfortunato ma solo l’inevitabile prezzo da pagare pur di riuscire a conquistare il maniero. D’altra parte se uno passeggia per la strada e si prende in pieno petto un proiettile sparato da un malvivente che all’uscita di una gioielleria si dovesse trovare ad affrontare una guardia armata, sarebbe da tutti considerato un uomo sfortunato.
Dato poi che, come sa benissimo chi conosce la statistica, la probabilità che due eventi indipendenti accadano è il prodotto delle probabilità dei due singoli eventi e che la probabilità è sempre un numero compreso fra zero ed uno, è evidente che la probabilità che due eventi rari si succedano è estremamente bassa e quindi maggiore è la sequenza di eventi improbabili che portano a conseguenze negative per qualcuno, maggiore è la sfortuna attribuita a quell’individuo.
Facciamo un esempio: esco dall’ufficio e torno a casa, ma sulla strada principale è caduto un grosso ramo a causa del recente temporale, per cui mi tocca deviare su una strada secondaria che conosco poco. Mi perdo e finisco su uno sterrato con la conseguente foratura di uno dei pneumatici. Mentre cerco di cambiare la gomma ricomincia a piovere, la visibilità si riduce quasi a zero e un SUV alla cui guida c’è un ragazzino mezzo ubriaco sbuca da dietro la curva e mi travolge in pieno. Iella nera, giusto? Com’era quella battuta nel classico di Mel Brooks «Frankenstein Junior»? «Potrebbe andare peggio: potrebbe piovere!»
La bassa probabilità non è tuttavia l’unico elemento che ci porta ad attribuire alla sfortuna un certo evento. Se l’evento in questione è anche inconsueto, e quindi non solo implicitamente raro, ma pure strano, imprevedibile, lontano dalla nostra esperienza quotidiana, allora l’attribuizione dello stesso alla mala sorte diventa ancora più verosimile. Nel caso fatto in precedenza, se invece di essere travolto da un SUV fossi stato assalito da una pantera nera scappata da un circo accampatosi nelle vicinanze, avrei potuto vincere facilmente la palma di “Sfigato dell’Anno”.
L’ultima parte della definizione è abbastanza ovvia: la sfortuna è un concetto antropocentrico. Se esplode una stella non diremo mai che i pianeti disabitati che orbitavano attorno ad essa sono stati “sfortunati”. La sfortuna si accanisce sugli individui, non sulle cose. Si tratta di un concetto legato al nostro confrontarci con il mondo circostante. Gli eventi che avvengono fra oggetti inanimati, a meno che non abbiano conseguenze negative su uno o più esseri umani, non ricadono sotto questo appellativo. Lo stesso vale per gli animali, a meno che con essi non si sia stabilito un forte legame empatico, come accade spesso con quelli domestici. Gli animali selvatici morti in un incendio non sono quindi considerati sfortunati ma lo potrebbe essere il cagnolino che, scappato dalla padrona, finisce sotto una macchina. In realtà spesso questi casi sono considerati sfortunati perché comunque si riflettono su un essere umano, quale ad esempio la padrona del cagnolino.
Inutile dire che per poter parlare di sfortuna, la connotazione degli eventi deve essere negativa, ovvero essi devono comportare un danno per qualcuno. Ovviamente la persona si dirà tanto più sfortuna quanto maggiore sarà l’entità del danno. A questo punto è abbastanza ovvio come possa essere definita per contro il concetto di “fortuna”:
Dicasi fortuna il verificarsi di uno o più eventi inconsueti o poco frequenti, le cui conseguenze abbiano un effetto positivo su uno o più individui.
Finalmente abbiamo a nostra disposizione due definizioni chiare e sufficientemente esaustive, almeno a livello qualitativo. Resta da definire l’aspetto quantitativo, ovvero, quanto inconsueta o infrequente deve essere un evento perché si possa parlare di sfortuna?
Qui entriamo nell’ambito della soggettività. Ci sono eventi che da un punto di vista scientifico sono considerati ad alta probabilità ma che nella percezione degli esseri umani vengono considerati rari e inaspettati. Un esempio sono gli eventi geologici come ad esempio i terremoti o le frane. Il nostro pianeta è in continuo cambiamento. tali cambiamenti, tuttavia, avvengono spesso su scale temporali per noi molto ampie. Così, eventi relativamente frequenti su scala geologica possono abbracciare molte generazioni e si sa che ne bastano anche solo tre o quattro perché la memoria storica si perda. Frane, terremoti, alluvioni, eventi meteorologici di grande entità possono a noi sembrare poco frequenti, specialmente in certe regioni del pianeta, ma non è detto che lo siano. Dunque la valutazione sulla rarità di un certo evento, quando parliamo di fortuna o sfortuna, va fatta nell’arco di una, al massimo due generazioni.
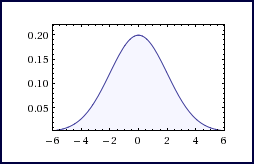
Distribuzione di Gauss (continua)
All’interno di questo periodo di tempo, la distribuzione di probabilità relativa a un singolo evento indipendente tende spesso ad avere una forma più o meno simmetrica, con un picco che fornisce la probabilità degli eventi più frequenti e una o due code che rappresentano quelli meno probabili. Le due distribuzioni più comuni sono la Gaussiana e la Poissoniana. La prima viene solitamente usata per descrivere variabili casuali a valori reali che tendono a concentrarsi attorno a un singolo valor medio. Un tipico esempio è il modo con il quale si distribuiscono i colpi attorno a un bersaglio. La seconda esprime le probabilità di un numero di eventi che si verifichino successivamente e indipendentemente in un dato intervallo di tempo, sapendo che mediamente se ne verifica un numero λ. Un tipico esempio di distribuzione di Poisson è relativa a come si distribuiscono le chiamate a un centralino nell’arco della giornata.
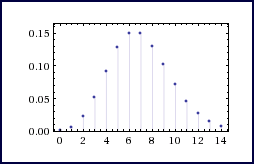
Distribuzione di Poisson (discreta)
In realtà esistono molte altre distribuzioni di probabilità, come quella uniforme, quella di Laplace, la distribuzione binomiale, quella esponenziale e via dicendo, non tutte con la stessa forma, ovvero con un picco e una o due code, ma la maggior parte degli eventi ai quali attribuiamo un significato in termini di buona o mala sorte, tendono a seguire quella di Gauss o di Poisson. Ne consegue che l’attribuire un evento al fato, vuole sostanzialmente dire definire un valore che isola un pezzo di coda, ovvero quella sezione della distribuzione di probabilità che rappresenta gli eventi meno frequenti, e prendere quindi tutti gli eventi corrispondenti a tale segmento di curva.
Quale sia questa soglia, di nuovo, è soggettivo, ma possiamo provare a darne una stima ragionevole in termini di sigma. Il termine sigma si riferisce allo scarto quadratico medio della distribuzione, ovvero alla stima di quanto sia più o meno disperso un insieme di dati attorno alla sua media. Se ad esempio tiro venti frecce su un bersaglio e quasi tutte finiscono più o meno al centro, la media sarà il centro e lo scarto quadratico medio sarà molto piccolo, dato che tutti i colpi sono concentrati. Se tuttavia questi si distribuissero su tutta la superficie del bersaglio, potrei ancora avere un valor medio nel centro — ovviamente sto parlando di media geometrica, non certo della media dei punteggi — ma la dispersione sarebbe molto alta e così lo scarto quadratico medio.
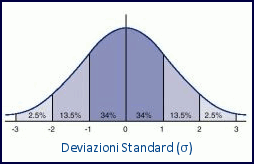
Distribuzione normale: sigma e percentuali
Nella Gaussiana, denominata anche distribuzione normale, una delle curve di distribuzione più utilizzate, la deviazione standard corrisponde al 68% dei possibili eventi, ovvero quelli a maggiore probabilità, addensati attorno al valor medio. Se prendessimo due sigma, l’area sottesa dalla curva rappresenterebbe oltre il 94% dei possibili eventi, e già a tre sigma avremmo il 99,73% di questi eventi, ovvero le code che rimangono fuori rappresenterebbero meno del 3 per mille dei possibili eventi, ovviamente quelli a più bassa probabilità. Arrivare a sei sigma vorrebbe dire tagliar via due code che rappresentano gli eventi con una frequenza inferiore a circa uno su seimila miliardi: decisamente rari!
Per concludere, volendo dare un valore di riferimento, almeno per quello che riguarda la distribuzione normale di probabilità, potremmo considerare fortunati o sfortunati, a seconda dei casi, quegli eventi che vanno oltre la soglia di tre sigma, decisamente fortunati o sfortunati, quelli oltre i sei.
A questo punto abbiamo tutto ciò che ci serve: due definizioni qualitative e un riferimento ragionevolmente verosimile di tipo quantitativo. Non resta che provare ad applicarle a casi reali e vedere se esiste di fatto una corrispondenza chiara fra la percezione che si ha di cosa sia fortunato e sfortunato, e la caratterizzazione e la distribuzione statistica degli eventi in gioco. Buon divertimento.




















Please use Facebook only for brief comments.
For longer comments you should use the text area at the bottom of the page.
Facebook Comments